使用任意精度数学的log（）算法示例

I'm looking to find an algorithm that I can implement in PHP to get the natural log() of an integer number using arbitrary precision maths. I'm limited by the PHP overlay library of the GMP library (see http://php.net/manual/en/ref.gmp.php for available GMP functions in PHP.)

If you know of a generic algorithm that can be translated into PHP, that would also be a useful starting point.

PHP supports a native log() function, I know, but I want to be able to work this out using arbitrary precision.

Closely related is getting an exp() function. If my schoolboy Maths serves me right, getting one can lead to the other.

Well you would have the Taylor series, that can be rewritten for better convergence 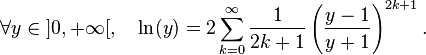$Improved taylor series of ln: 2 sum_{k=0..+inf} 1/(2k+1) * ((y-1)/(y+1))^(2k+1)$

To transform this nice equality into an algorithm, you have to understand how a converging series work : each term is smaller and smaller. This decrease happens fast enough so that the total sum is a finite value : ln(y).

Because of nice properties of the real numbers, you may consider the sequence converging to ln(y) :

L(1) = 2/1 * (y-1)/(y+1)
L(2) = 2/1 * (y-1)/(y+1) + 2/3 * ( (y-1)/(y+1) )^3
L(3) = 2/1 * (y-1)/(y+1) + 2/3 * ( (y-1)/(y+1) )^3 + 2/5 * ( (y-1)/(y+1) )^5

.. and so on.

Obviously, the algorithm to compute this sequence is easy :

x = (y-1)/(y+1);
z = x * x;
L = 0;
k = 0;
for(k=1; x > epsilon; k+=2)
{
    L += 2 * x / k;
    x *= z;
}

At some point, your x will become so small that it will not contribute to the interesting digits of L anymore, instead only modifying the much smaller digits. When these modifications start to be too insignificant for your purposes, you may stop.

Thus if you want to achieve a precision 1e^-20, set epsilon to be reasonably smaller than that, and you're good to go.

Don't forget to factorize within the log if you can. If it's a perfect square for example, ln(a²) = 2 ln(a) Indeed, the series will converge faster when (y-1)/(y+1) is smaller, thus when y is smaller (or rather, closer to 1, but that should be equivalent if you're planning on using integers).