Liner programm 中如何把实际问题转化成方程组。
Food Distribution No Poverty and Zero Hunger are listed as the top two Sustainable Development Goals by the United Nations. Food rescue service provides a promising way to reduce food waste, overcome food insecurity and improve environmental sustainability. Organizations providing food rescue service rescue the surplus food from different food providers and redistributing to local communities that are in need of food. For questions 6 and 7, you will help a food rescue organization FS to decide how to redistribute the food in an efficient way. The problem is abstracted in the following way: There are M food providers (referred to as providers) and N local communities in need of food (referred to as communities). Community j needs at least Cj integer units of food. The transportation cost per unit of food from provider i to community j is Ti,j. When transporting food from a provider to a community, trucks cannot be overweight. All trucks have the same weight limit per truck, and only one truck moves between provider i and community j. The food coming from provider i has weight Wiper unit. We need to determine the integer number of food units to transport from each provider to each community, while meeting the above constraints and minimizing transportation costs.
针对文中的问题,写了个简单的python程序
import pulp as pulp
# 决策变量
# T1-T6,对应表中提供者(provider)向组织(community)运送的食物单位数
# 例如:T1是DunKin Donuts向Gates运送的食物单位数
# T2表示DunKin Donuts向Sorrells运送的食物单位数...从左到右 从上到下...
# T6表示Underground向Sorrells运送的食物单位数
# 目标函数
# 运输成本最小 12*T1+20*T2+4*T3+5*T4+2*T5+1*T6
# 约束条件
# T1+T3+T5=15(吃饱)
# T2+T4+T6=30(吃饱)
# 1.2*T1<=30(不超重)
# 1.2*T2<=30(不超重)
# 1.3*T3<=30(不超重)
# 1.3*T4<=30(不超重)
# 1.1*T5<=30(不超重)
# 1.1*T6<=30(不超重)
def wordProblemIP():
"""
方程组
:return:
"""
VAR_NUM = 6
# 决策变量共6个
variables = [pulp.LpVariable('X%d' % i, lowBound=0, cat=pulp.LpInteger) for i in range(0, VAR_NUM)]
# 目标函数
c = [12, 20, 4, 5, 2, 1]
objective = sum([c[i] * variables[i] for i in range(0, VAR_NUM)])
# 约束条件
constraints = []
constraints.append(variables[0] + variables[2] + variables[4] == 15)
constraints.append(variables[1] + variables[3] + variables[5] == 30)
constraints.append(variables[0] * 1.2 <= 30)
constraints.append(variables[1] * 1.2 <= 30)
constraints.append(variables[2] * 1.3 <= 30)
constraints.append(variables[3] * 1.3 <= 30)
constraints.append(variables[4] * 1.1 <= 30)
constraints.append(variables[5] * 1.1 <= 30)
return objective, constraints
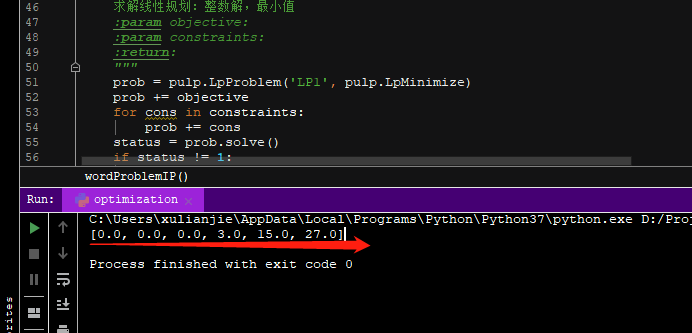
def solveIP(objective, constraints):
"""
求解线性规划:整数解,最小值
:param objective:
:param constraints:
:return:
"""
prob = pulp.LpProblem('LP1', pulp.LpMinimize)
prob += objective
for cons in constraints:
prob += cons
status = prob.solve()
if status != 1:
return None
else:
return [v.varValue.real for v in prob.variables()]
if __name__ == '__main__':
obj, cons = wordProblemIP()
print(solveIP(obj, cons))
我的运行结果: